L15 Inheritance of Complex Quantitative Traits

一、Frequency Distributions

Some Definitions

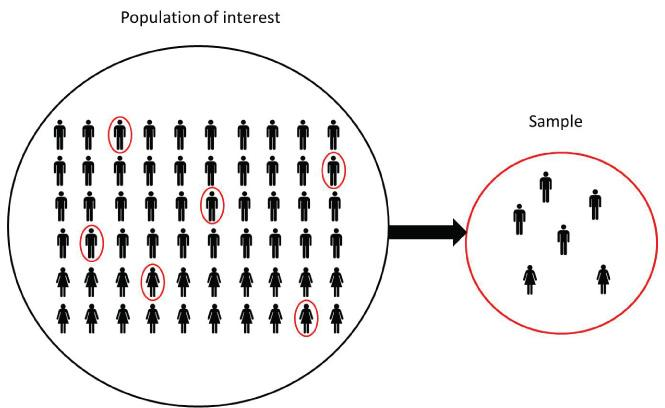
1. Population

Population: Group of individuals interested

2. Sample

Sample: only a small fraction of all the individuals in the population can be measured. We call this group the sample.

3. Frequency Distribution

Frequency distribution: is a list, table or graph that displays the frequency of various outcomes in a sample.

Histogram 柱状图

4. Mean or Average 平均值

平均数，统计学术语，是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。

$$
\overline{x} = \frac{x_1 + x_2 + ··· \ + x_n}{n}
$$

5. Median 中位数

中位数，又称中点数，中值。中位数是按顺序排列的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比他大，有一半的数据比他小

6. Mode 众数

众数（Mode）是指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。 也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。用M表示。

7. Model Class

The modal class in a sample is the class that contains the most observations.

8. Variance 方差

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数

Variance 方差: to measure the spread of data in a frequency distribution

The sample variance, denoted $S^2$ , is calculated from the formula
$$
s^{2} = \frac{\sum (X_{k} - \overline{X})^{2}}{n - 1}
$$

9. standard deviation 标准差

标准差（Standard Deviation） ，中文环境中又常称均方差，是离均差平方的算术平均数的平方根，用σ表示。在概率统计中最常使用作为统计分布程度上的测量。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

$$
s = \sqrt{s^{2}}
$$

二、Quantitative And Qualitative Traits

The Definition

1. Complex / Quantitative Trait 数量性状

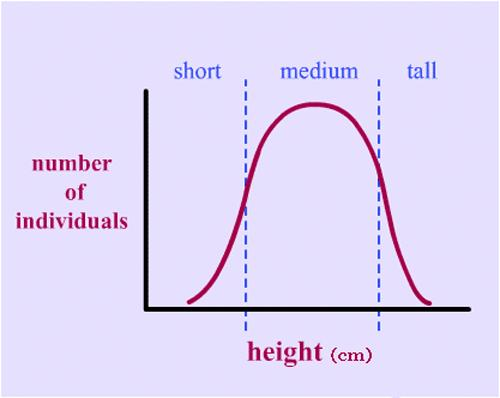
A quantitative trait is a measurable phenotype that depends on the cumulative actions of many genes and the environment.

These traits can vary among individuals, over a range, to produce a continuous distribution of phenotypes.

Examples include aspects of morphology (height, weight); physiology (blood pressure); behavior (aggression); as well as molecular phenotypes (gene expression levels, high- and low-density cholesterol levels).

Quantitative traits do not behave according to simple Mendelian inheritance laws.

Individuals cannot be classified by discrete values

Quantitative trait distribution show a continuous range of variation

Complex mode of inheritance

Moderate to great environmental effect

2. Mendelian / Qualitative traits 孟德尔性状/质量性状

Mendelian traits/Qualitative traits

Phenotype with discrete and easy to measure values

Individuals can be correctly classified according to phenotype

Show mendelian inheritance

Little environmental effect

Example of Quantitative Traits

1. Polygenetic in wheat grains color

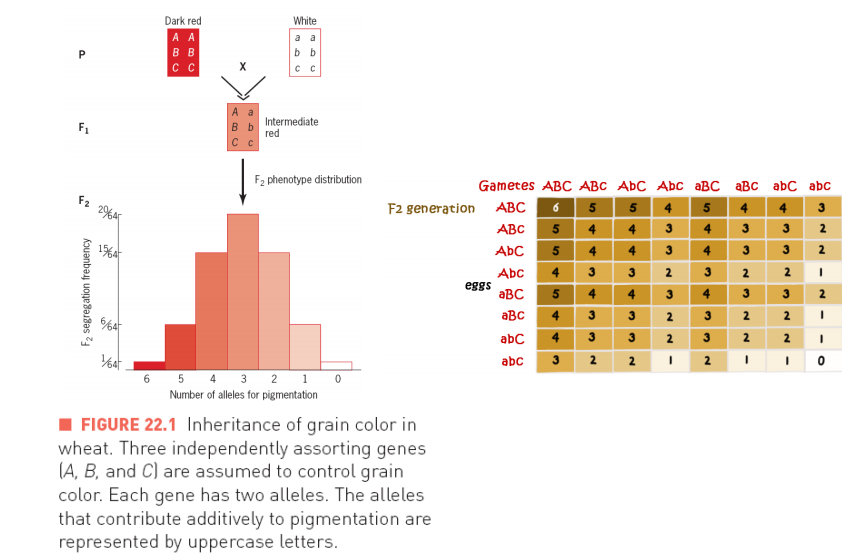
■ FIGURE 22.1 Inheritance of grain color in wheat. Three independently assorting genes [A, B, and C] are assumed to control grain color. Each gene has two alleles. The alleles that contribute additively to pigmentation are represented by uppercase letters.

2. Length of The Corolla In Tobacco Flowers (Studied By Edward M. East)

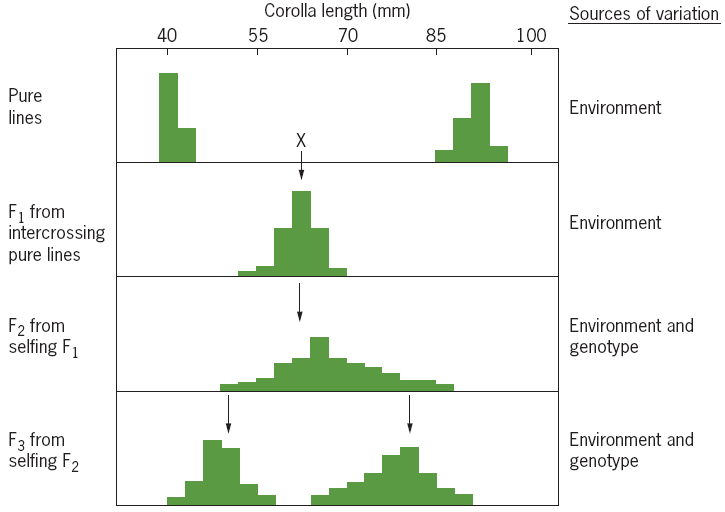
This variability if F2 was due to two sources:

1. the segregation and independent assortment of different pairs of alleles controlling corolla length, and

2. environmental factors.

The reduced amount of variation within the F3 lines was presumably due to the segregation of fewer allelic differences.

Edward M. East had studied 444 F2 plants and failed to find even one with either of the parental phenotypes.

This failure would seem to rule out (排除) the hypothesis of four or fewer genes controlling corolla length.

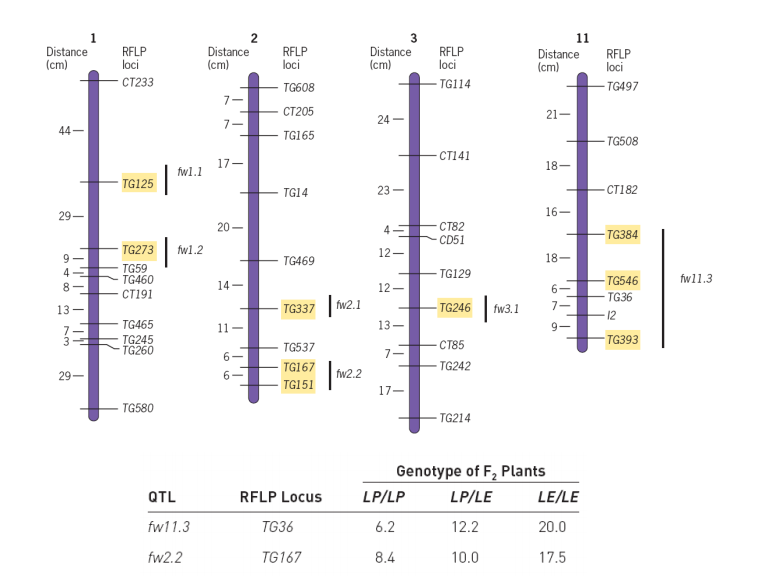
Quantitative Trait Loci

the locus for a gene that influences a quantitative trait is called a quantitative trait locus (QTL).

QT loci have been identified and mapped on specific chromosomes in model laboratory organisms

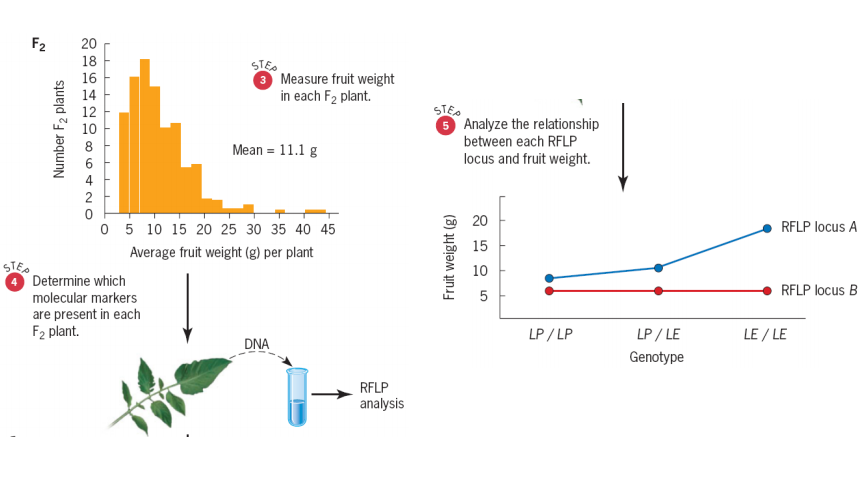
1. RFLPs

restriction fragment-length polymorphisms, RFLPs (限制性片段长度多态性)

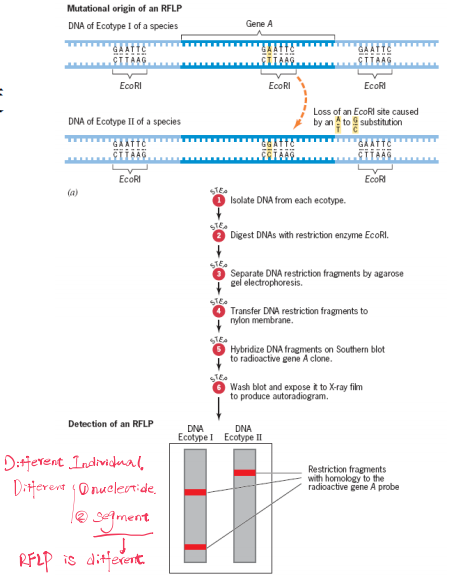
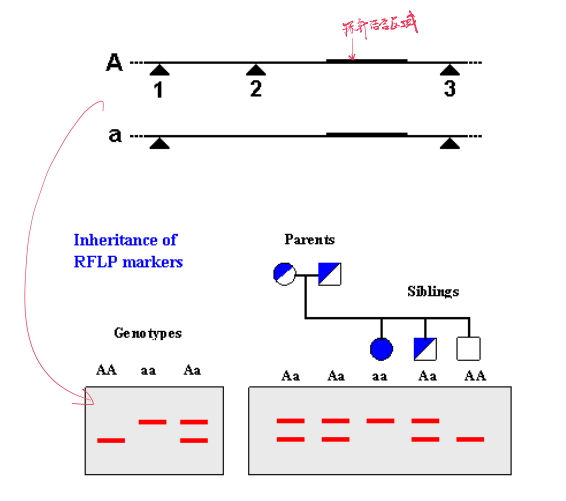
2. RFLP And Quantitative Trait Loci

Steven D. Tanksley exploited the fact that L. pimpinellifoliumand L. esculentum differ in the sites where restriction enzymes cleave genomic DNA. (RFLPs)

三、The Multiple Factor Hypothesis

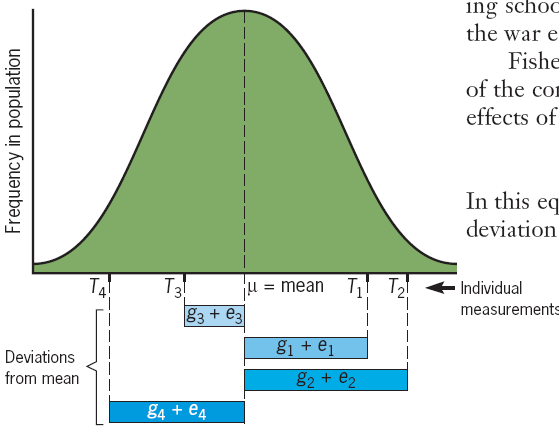
$\mu$, $g$, $e$ And $T$

The key idea in quantitative genetics is that traits are controlled by many different factors in the environment and in the genotype.

• $\mu$ represents the population mean,

• g represents the deviation from the mean that is due to genetic factors, and

• e represents the deviation from the mean that is due to environmental factors.

$$
T = \mu + g + e
$$

Partitioning the Phenotypic Variance 表型变异的划分

1. Definition

$V_T$ total phenotypic variance

$V_g$ genetic variance

$V_e$ environmental variance
$$
V_{T} = V_{g} + V_{e}
$$

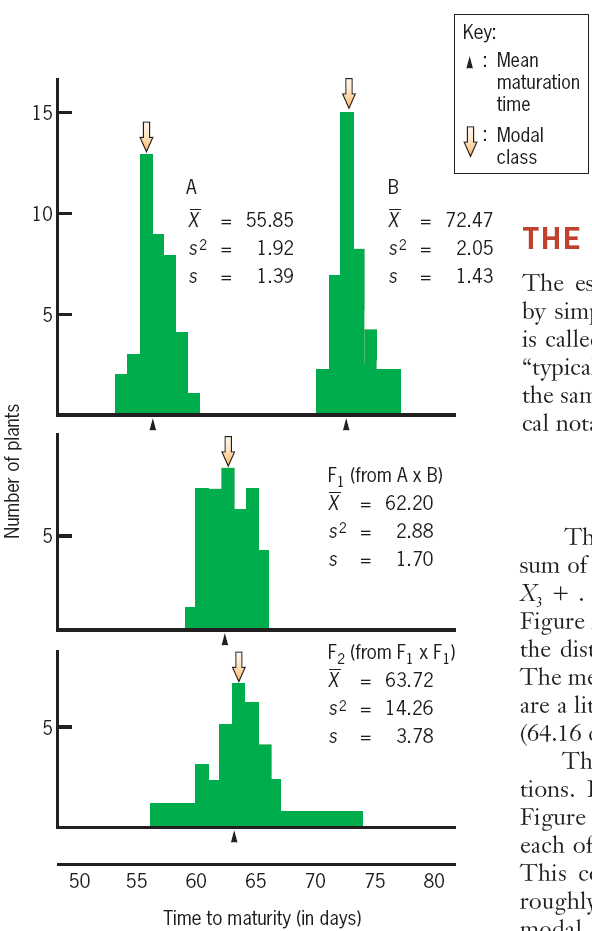
2. Example Calculation

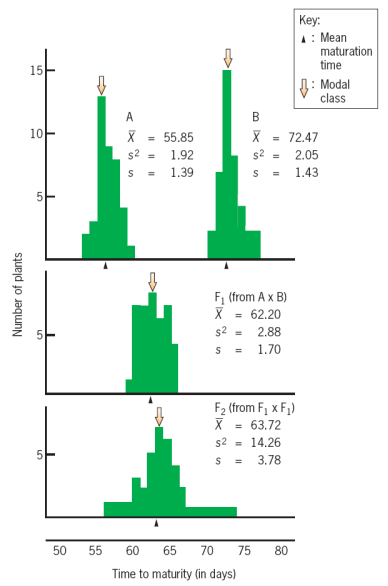
$$
V_{e} = (V_{A} + V_{B} + V_{F1})/3 \ = (1.92\ days^{2} + 2.05\ days^{2} + 2.88 \ days^{2})/3 \ =2.28\ days^{2}
$$
The $V_e$ Average represents the varients of environment

假设F2的生长环境与F1，A，B相同：
$$
\because V_{T} = V_{g} + V_{e} \
\therefore V_{g} = V_{T} - V_{e} \
= 14.26\ days^{2} - 2.28\ days^{2} \
= 11.98\ days^{2}
$$

3. Broad-sense Heritability 广义遗传性

$$
H^{2} = V_{g} / V_{T} \
V_{g} / (V_{g} + V_{e})
$$

For F2 wheat population
$$
V_{T} = V_{g} + V_{e}
$$

$$
14.26\ days^{2} = 11.98\ days^{2} + 2.28\ days^{2}
$$

$$
H^{2} = 11.98/14.26 = 0.84
$$

In this population 84% of the observed variability in wheat maturation time is due to genetic differences among individuals.

$H^{2}$ 代表由gene贡献的“差异”的比例

4. Narrow-sense Heritability 狭义遗传性

Genetic variance has three major components: the additive genetic variance (加性遗传方差), dominance variance (显性方差), and epistatic variance (上位方差)

• Additive genetic variance involves the inheritance of a particular allele from your parent and this allele’s independent effect on the specific phenotype, which will cause the phenotype deviation from the mean phenotype

• Dominance genetic variance refers to the phenotype deviation caused by the interactions between alternative alleles that control one trait at one specific locus.

• Epistatic variance involves an interaction between different alleles in different loci

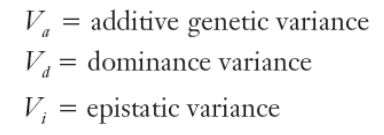
$$
V_{g} = V_{a} + V_{d} + V_{i}
$$

$$
\therefore V_{T} = V_{a} + V_{d} + V_{i} + V_{e}
$$

$$
h^{2} = V_{a} / V_{T}
$$

The closer $h^{2}$ is to one, the greater is our ability to predict an offspring’s phenotype.

Thus, if we knew the parental phenotypes, we would be better able to predict the height of a human’s offspring than the litter size of a pig’s offspring.

五、Predicting Phenotypes

Example Calculation: IQ

the narrow-sense heritability of IQ has been estimated to be about $h^{2}$=0.4 — that is, about 40% of the observed variation in IQ scores is due to the additive effects of alleles.

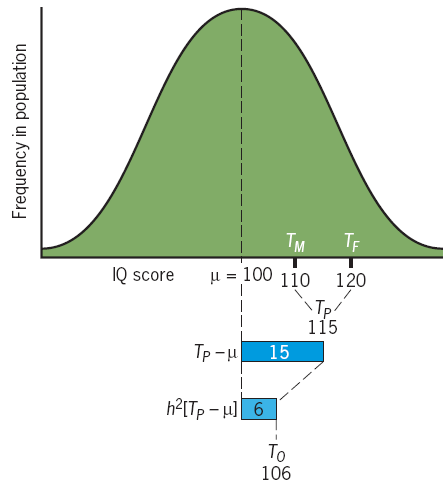$$ T_{o} = \mu + h^{2}[(T_{M} + T_{F})/2 - \mu] $$ $T_{o}$ is the mean of the offspring, $\mu$ is the mean of the overall population

$T_{s}$ is the mean of the selected parents, and $h^{2}$ is the narrow-sense heritability.

$(T_{M} + T_{F})/2$ is usually called the midparent value (中间价)
$$
\therefore T_{o} = h^{2} [T_{P} - \mu]
$$

$$
\therefore T_{o} = 100 + (0.4)[115 - 100] = 106
$$

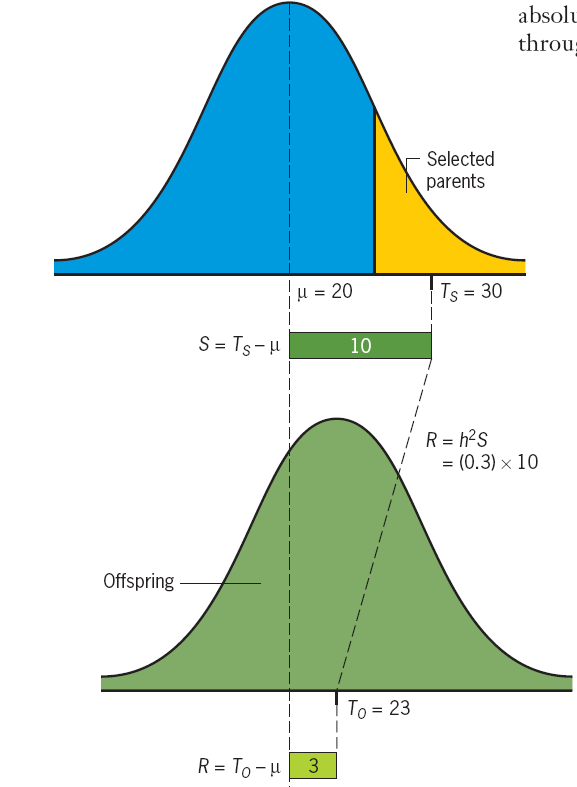
Artificial Selection

$T_{o} = h^{2} [T_{P} - \mu]$ , this equation allows us to predict how the mean of the population will change by selecting the individuals that will be parents. We call this process artificial selection.
$$
[T_{o} - \mu] = h^{2} [T_{s} - \mu]
$$

$$
R = h^{2} S
$$

S: selection differential 选择差异

R: the response to selection

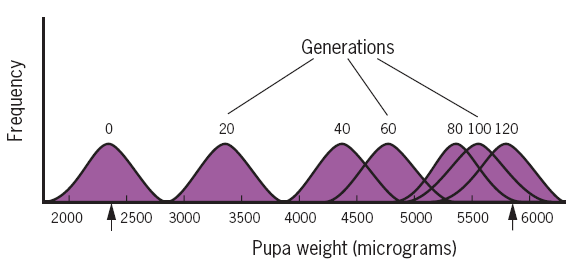
Frequency distributions of pupa weight in Tribolium populations selected for increased size. The shape of the distributions is only approximate. The means at generations 0 and 120 are indicated by arrows.