L14 Population Genetics
一、The Introduction to Population Genetics
Population genetics studies genes in groups of individual.
Populations in Genetic Equilibrium (allele frequencies no longer change)
Allele Frequencies And Genotype Frequencies
1. Introduction to Allele Frequencies
It is the number of copies of a particular allele divided by the number of copies of all alleles at the genetic place (locus) in a population
2. Estimation of Allele Frequencies
$$
\text{Frequencies of an allele = } \frac{\text{Numbers of copies of a particular allele}}{\text{Numbers of copies of ALL alleles}}
$$
Suppose p is the allele frequency of one allele, and q is the allele frequency of the other allele
Then
$$
p + q = 1
$$
3. Introduction to Genotype Frequencies
Is the number of individuals with a given genotype divided by the total number of individuals in population.
二、The Hardy-Weinberg principle
Introduction of The Principle
Describes a mathematical relationship between allele frequencies and genotype frequencies.
Allows the prediction of a population’s genotype frequencies from its allele frequencies.
Assume that in a population, a particular gene segregates two alleles, A and a, with frequencies of p and q, respectively.
If members of the population mate randomly,
- The diploid genotypes of the next generation will be formed by the random union of haploid eggs and haploid sperm.
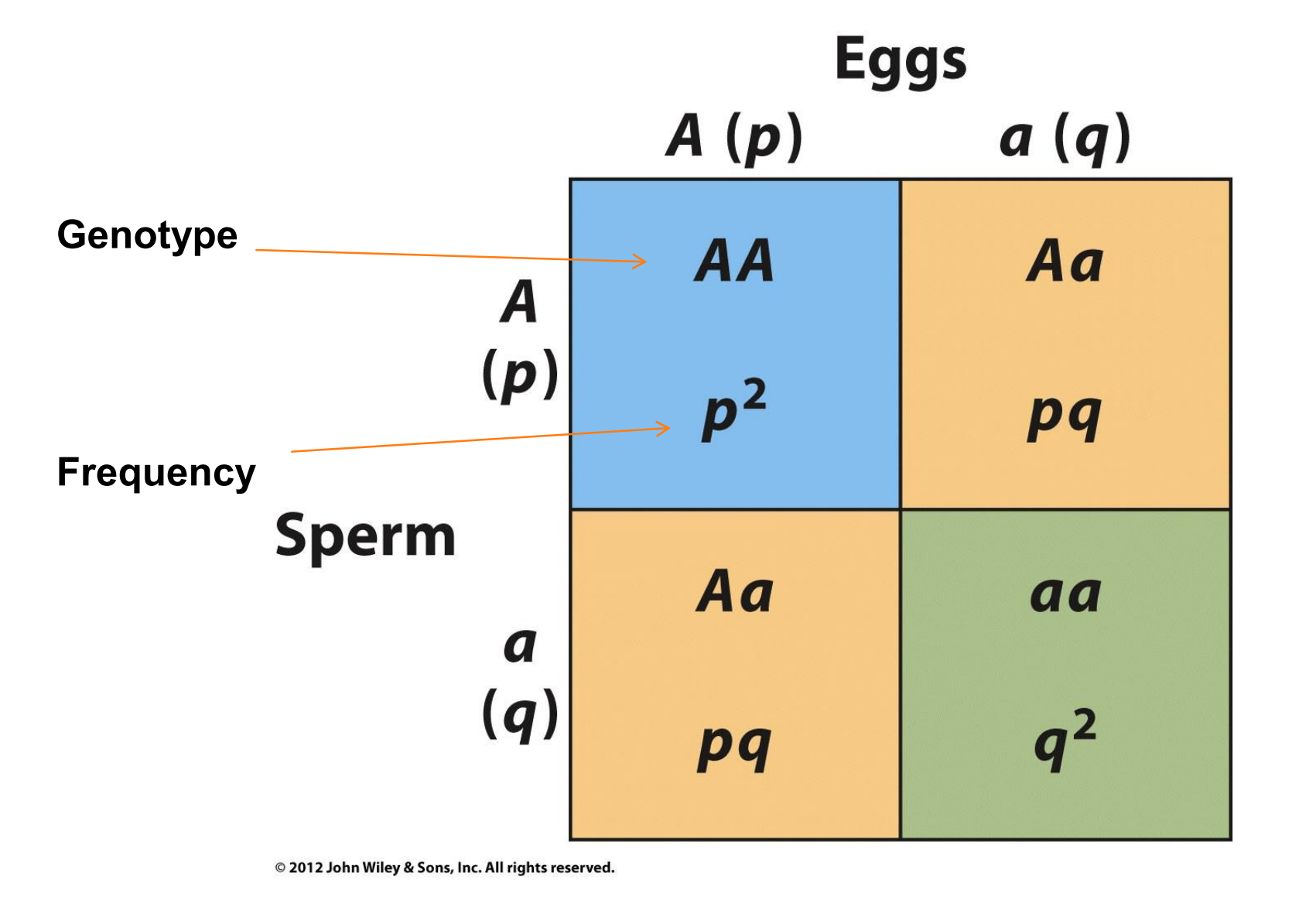
- The probability of producing an AA homozygote is $p \cdot p = p^{2}$.
- The probability of producing an aa homozygote is $q \cdot q = q^{2}$
- A heterozygote may be produced by
- an A sperm uniting with an a egg and
- an a sperm uniting with an A egg
- Each of these events occurs with probability $ p \cdot q$, so the total probability of forming an Aa zygote is $2pq$.
These predicted frequencies can be obtained by expanding the binomial expression
$$
(p + q)^{2} = p^{2} + 2pq + 2q^{2}
$$
Hardy-Weinberg Equilibrium
1. Introduction
The key assumption underlying the Hardy-Weinberg principle is random mating.
If no differential survival or reproduction exists among members of the population,
- the Hardy-Weinberg genotype frequencies persist generation after generation.
- the genotype is expected to produce $p^{2} + 2pq + q^{2}$
- the population is at equilibrium.
This condition is Hardy-Weinberg equilibrium.
Mutation、migration、natural selection、random genetic drift can influence this equilibrium(causes changes in the frequencies)
2. Prediction
In the equilibrium, we can predict allele frequencies from the genotype frequencies and can also predict genotype frequencies from the allele frequencies.
The Hardy-Weinberg Principle for X-Linked Genes
For X-linked genes, allele frequencies are estimated from the frequencies of the genotypes in males.
Example: Color Vision

For Multiple Alleles
Genotypes can be calculated by expanding trinomial
$$
(p + q + r)^{2} = p^{2} + q^{2} + r^{2} + 2pq + 2qr + 2pr
$$
Example: Blood type

三、Exceptions to the Hardy-Weinberg Principle
The cases that will disrupt Hardy-Weinberg equilibrium (…the genotype or allele frequencies will not persist generation after generation)
Non-random Mating
Nonrandom mating includes
- Consanguineous mating (mating between genetically related individuals,近亲结婚)
- Assortative mating (mating between individuals with similar phenotypes,选型交配)
Both consanguineous mating and assortative mating reduce the frequency of heterozygotes and increase the frequency of homozygotes.
The effects of consanguineous mating can be quantified using the inbreeding coefficient (近交系数), F.

F = 0 ~ 1
F = 1时:For a population that is completely inbreeding or Self-fertilization

Unequal Survival
If zygotes produced by random mating have different survival rates
Heterozygotes ≠ Homozygotes
A sample of 200 adults yielded the following data:

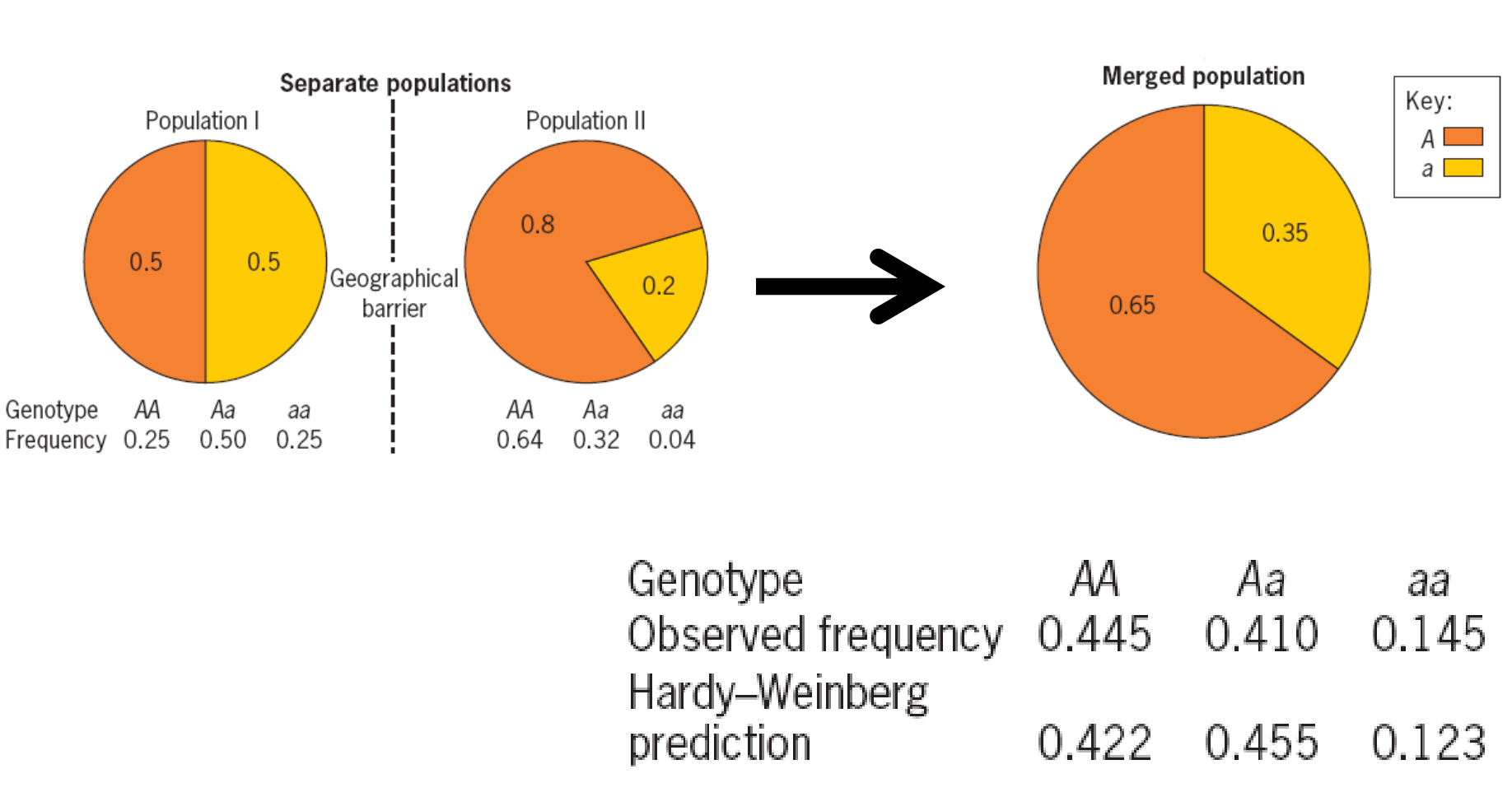
Population Subdivision 种群分化/种群破碎化
In nature, populations may be subdivided due to geographical or ecological barriers (地理或生态障碍) that may be correlated with genetic differences.
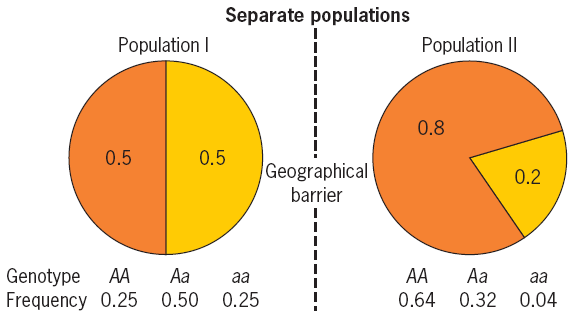
Migration
The introduction of genes by recent migrations can alter allele and genotype frequencies within a population and
disrupt Hardy-Weinberg equilibrium
四、Natural Selection – (systematic changes-differential survival and reproduction)
According to Charles Darwin: “the Origin of Species by Means of Natural Selection“, published in 1859
- Organisms produce more offspring than the environment can support
- Only some of them can survive and reproduce
- After many generations of such competition, traits associated with strong competitive ability become prevalent in the population
Selection for survival and reproduction in the face of competition is therefore the mechanism that changes the physical and behavioral characteristics of a species. This process was called natural selection.
The Concept of Fitness
Fitness is the ability to survive and reproduce is a phenotype and that it is determined, at least partly, by genes.
Geneticists refer to this ability to survive and reproduce as Fitness.
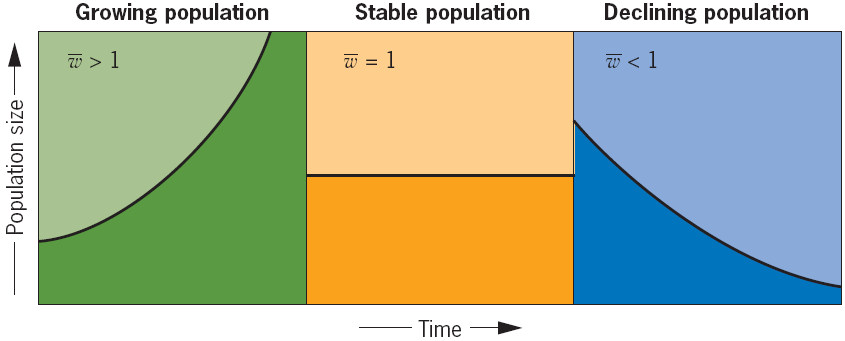
Each member of a population has its own fitness value
- w = 0 if it dies or fails to reproduce,
- w = 1 if it survives and (on average) produces 1 offspring,
- w = 2 if it survives and (on average) produces 2 offspring,
- and so forth.
Natural Selection at the Level of the Gene
Example: Color of moss

assume that fitness is determined by a single gene , in a particular species of insect.
alleles, A for dark in color and a for light in color. A is dominant
Coefficient can be separated to relative fitness and selection coefficient

Natural Selection at the Level of the Gene
The initial genetic composition of the population:
- Suppose A with p = 0.5, and a with q = 0.5, and that s2 = 0.1.
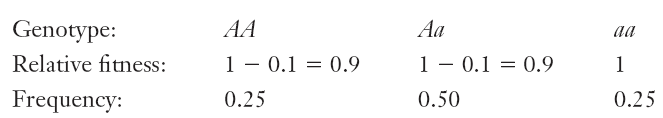
In forming the next generation, each genotype will contribute gametes in proportion to its frequency and relative fitness.

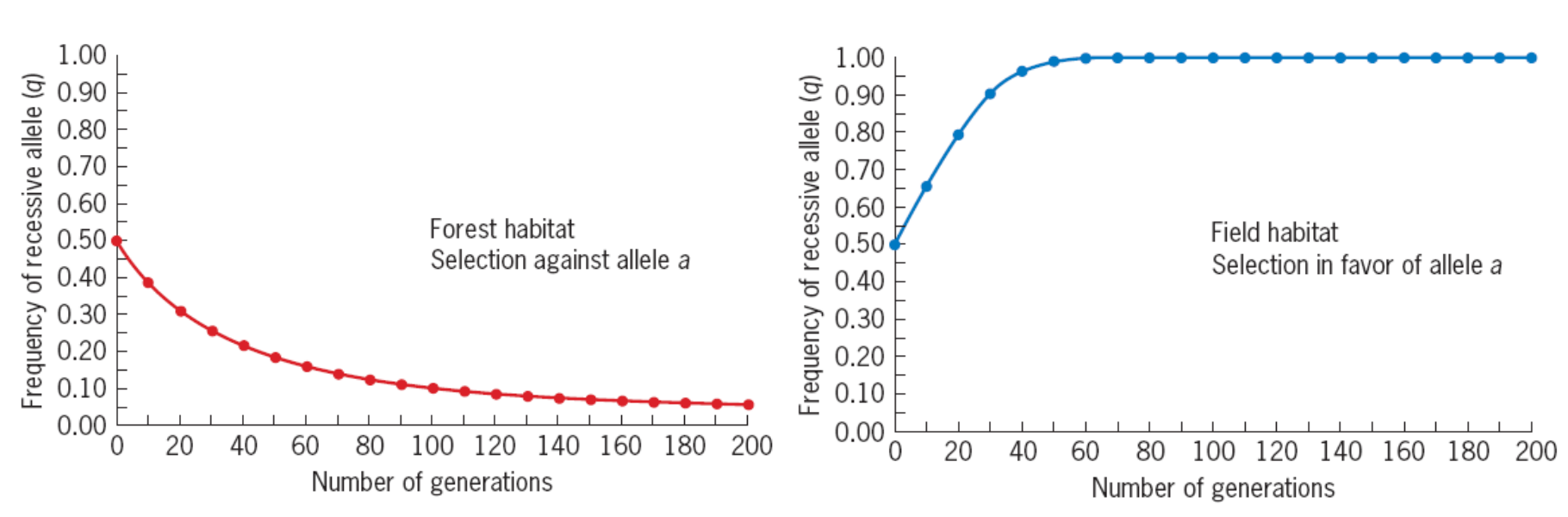
q (G2) = 0.270 + 0.487/2 = 0.513 > q (G1) = 0.5
Every generation afterward, the freauency of a will rise, and eventually it will equal 1, at which point we can say that the allele has been fixed in the population.
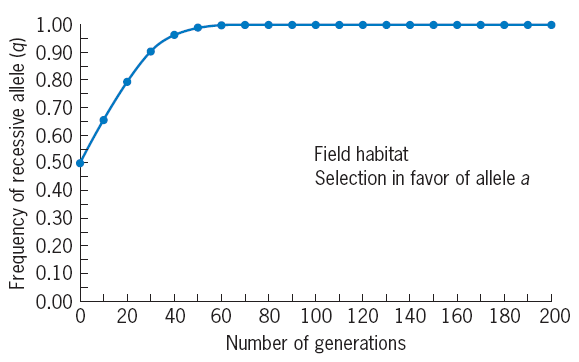
Selection for a recessive allele—and therefore against a harmful dominant allele—is more effective than selection
against a recessive allele.
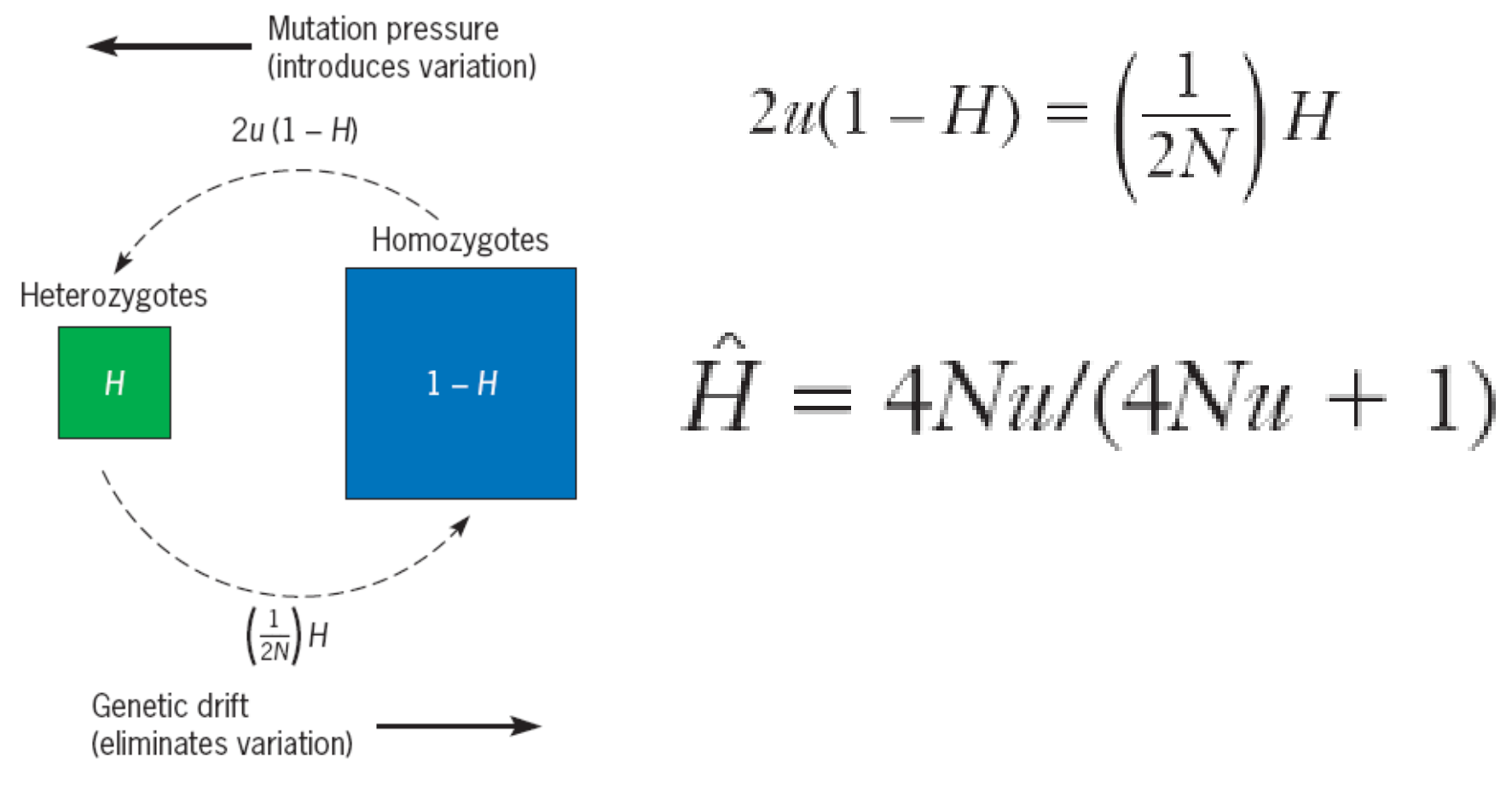
五、Random Genetic Drift
Introduction
Natural selection as a systematic force in evolution. However, evolution is affected by random processes.
Allele frequencies change unpredictably in populations because of uncertainties during reproduction.
- Mutation is a random process that profoundly affects evolution
- Genetic drift, the random change of allele frequencies in populations, due to uncertainties in Mendelian segregation.
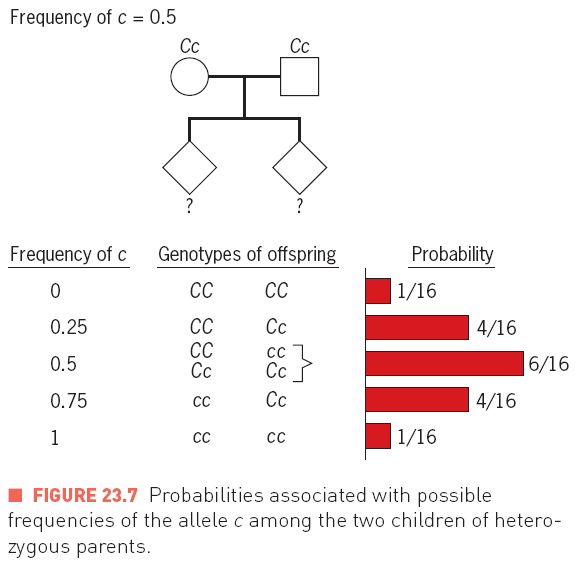
Genetic drift, the random change of allele frequencies in populations, due to uncertainties in Mendelian
segregation.
Thus, the genetic composition of the population can change even without the force of natural selection.
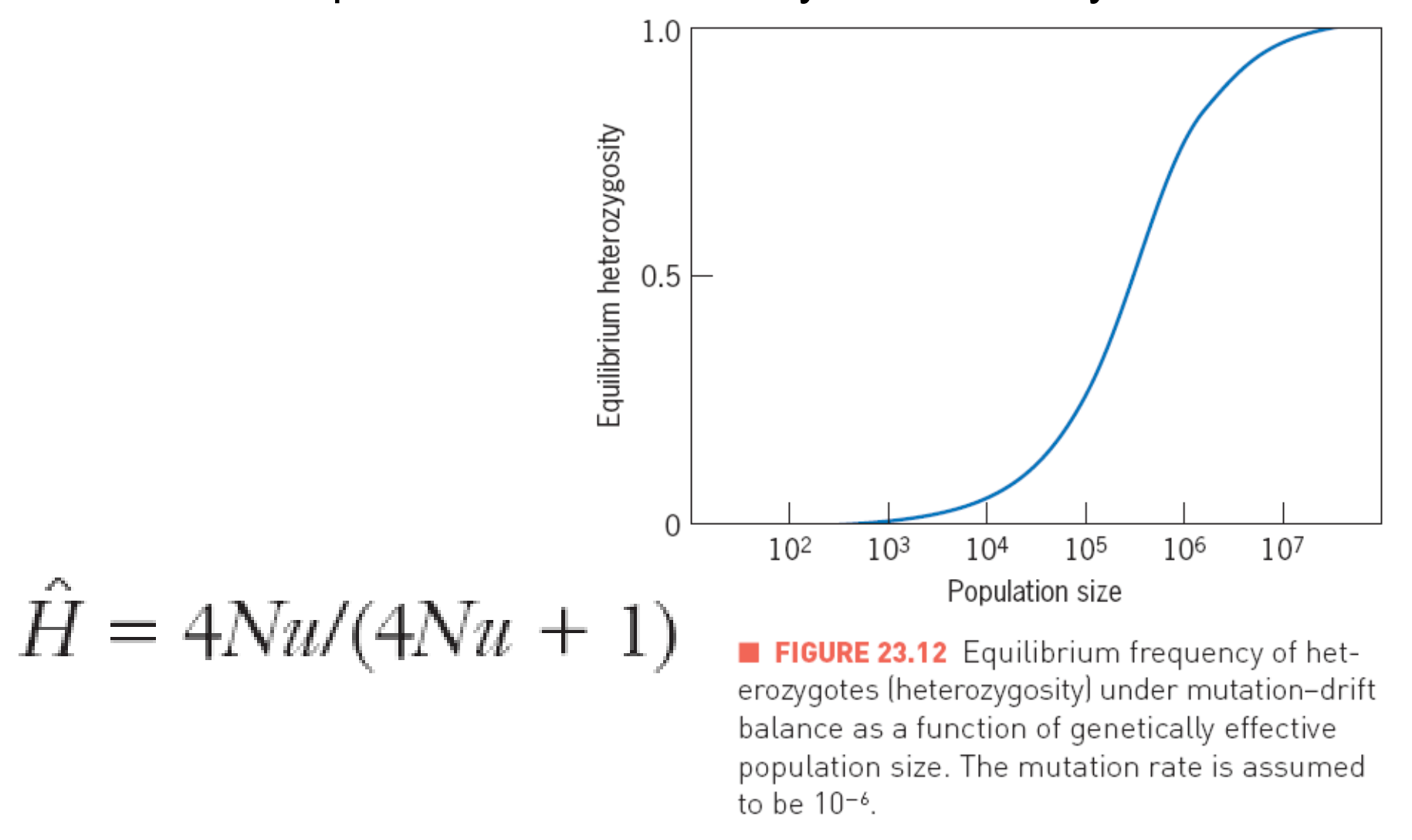
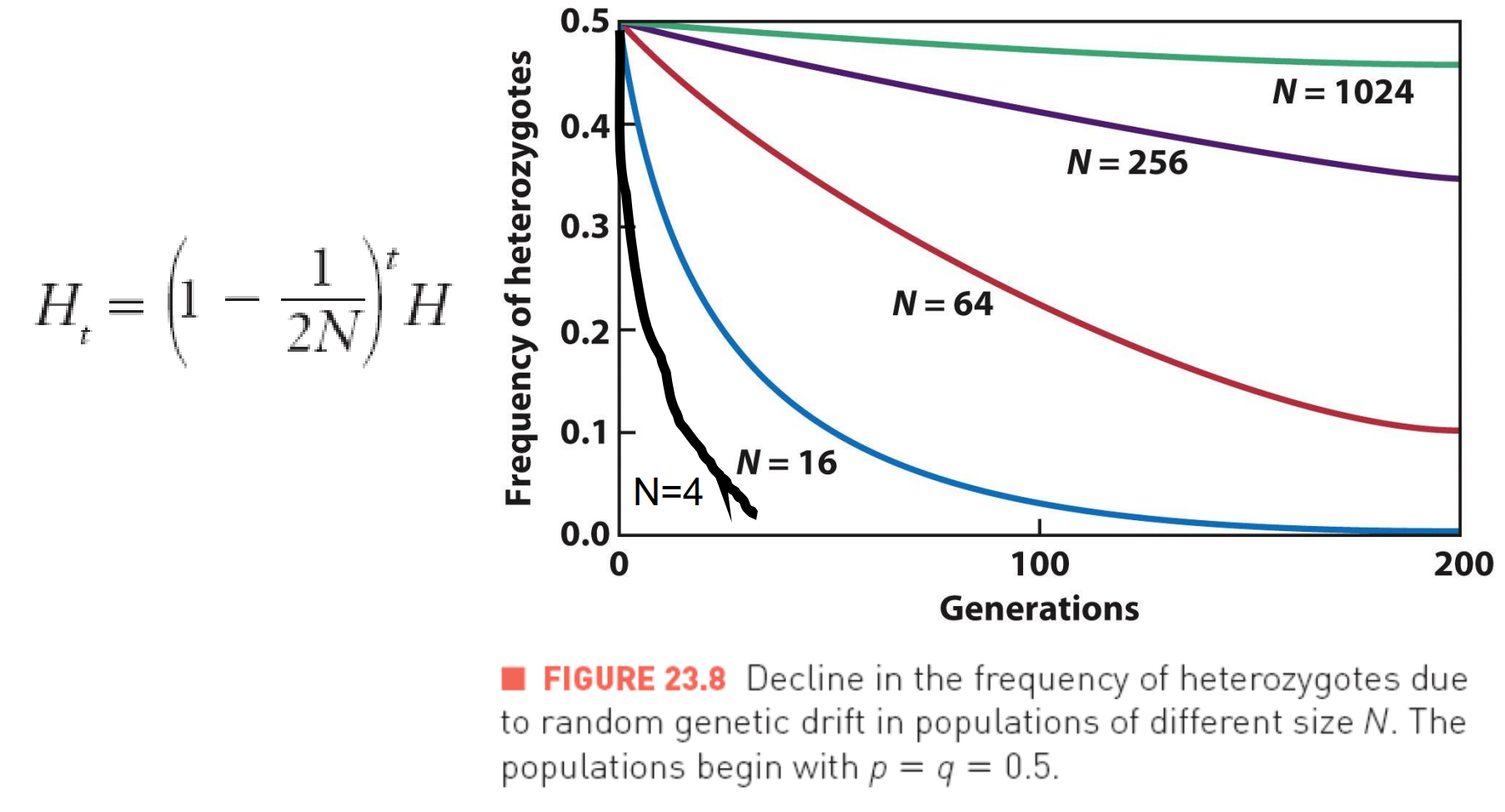
The Effects of Population Size
In large populations, the effect of genetic drift is minimal.
$$
\text{HWE: }(p + q)^{2} = p^{2} + 2pq + q^{2}
$$
In small populations, genetic drift may be the primary evolutionary force.
The effect of population size is determined by monitoring the frequency of heterozygotes, or the heterozygosity of a population over time. Represented with H
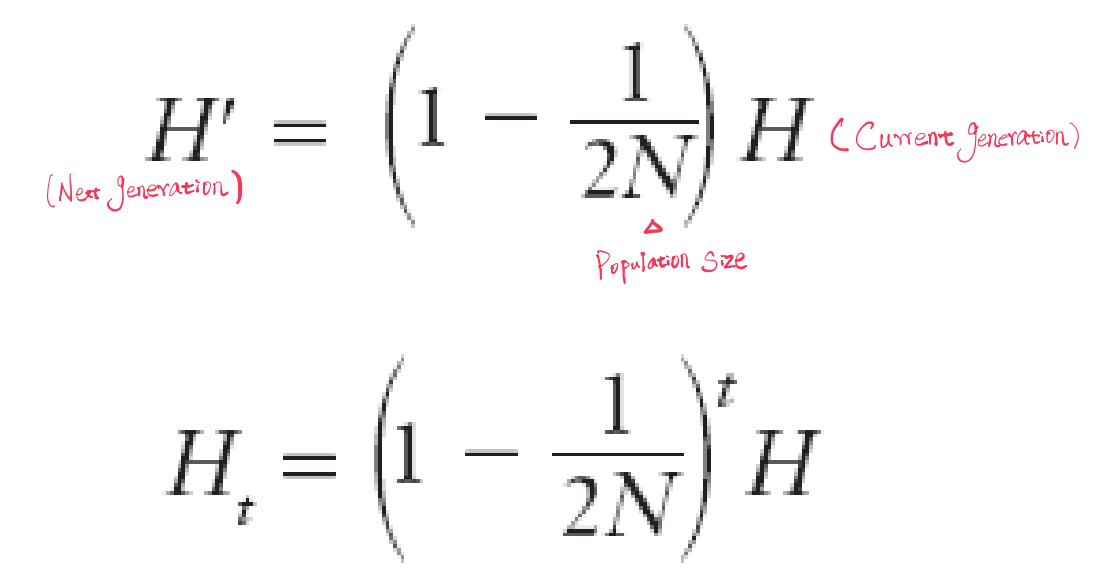
In large populations, the effect of genetic drift is minimal.
In small populations, genetic drift may be the primary evolutionary force.
Hardy-Weinberg equilibrium:
In a randomly mating population
without natural selection or genetic drift to change allele frequencies,
and without migration or mutation to introduce new alleles
The real population:
- these evolutionary forces may act in contrary ways to create a dynamic eauilibrium, in which there is no net change in allele frequencies.
Dynamic equilibrium can be caused by:
- Balancing Selection
- Mutation-selection Balance
- Mutation-drift Balance
1. Balancing Selection 平衡选择
Balancing selection also called heterozygote advantage(杂合优势)
The selection favors the heterozygotes at the expense of each type of homozygote in the population.
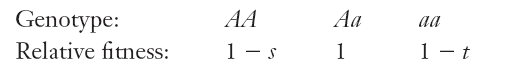
At the balance point, the frequency of A is p = t / (s + t), and the frequency of a is q = s / (s + t)
Deduction of Equilibrium Circumstances

$$
\text{The Average Fitness: } \overline{w} = (1 - s) \times p^{2} + 1 \times (2pq) + (1 - t) \times q^{2} \
\because p + q = (p + q)^{2} = 1 \
\therefore \overline{w} = 1 - sp^{2} -tq^{2}
$$
$$
\text{Frequency of A in the next generation after selection:} p’ = \frac{p^{2}(1-s) + \frac{1}{2} \cdot 2pq}{ \overline{w} } \
\because p + q = 1 \
\therefore p’ = \frac{p(p+q)-sp^{2}}{\overline{w}} =\frac{p(1 - sp)}{\overline{w}}
$$
$$
\text{Change in frequency of A due to selection:}\Delta p = p’ - p = p (\frac{1-sp}{1} -1) =p \cdot \frac{1-sp^{2}-tq^{2}}{\overline{w}} = p \cdot 1 = p \
\because \overline{w} = 1 - sp^{2} -tq^{2} \
\therefore \Delta p = p \cdot \frac{1-sp^{2}-tq^{2}}{\overline{w}} = p \cdot 1 = p
$$
$$
\text{At equilibrium: } \Delta p = 0 \
\therefore \frac{1 - sp}{\overline{w} } = 1 \
\therefore sp = sp^{2} + tq^{2} \
\therefore
p = \frac{t}{s + t},\ q = \frac{s}{s + t}
$$
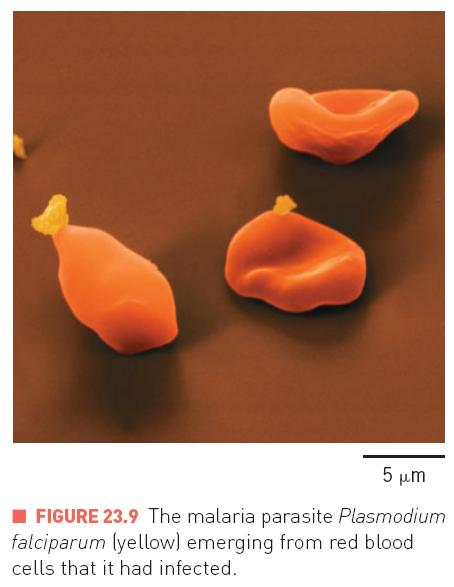
Example: malaria parasite
The malaria parasite Plasmodium falciparum (yellow) emerging from red blood cells that it had infected.
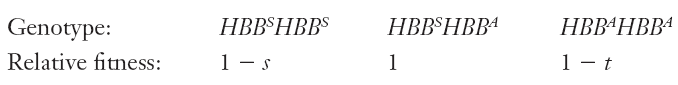
$$
\text{Suppose s = 1, p = 0.1} \ p = \frac{t}{s+ t} \ \therefore t = (0.1)/(0.9) = 0.11
$$
2. Mutation-Selection Balance 突变-选择平衡
Mutation-selection balance:
- the rate at which deleterious recessive alleles are created by mutation
- equals the rate at which deleterious alleles are eliminated by selection.


At Equilibrium
$$
\Delta q_{s} = - \frac{sq^{2} p}{1 - sq^{2}}
$$
$$
\Delta q_{mu} = \mu p
$$
$$
\text{At equilibrium: } \Delta q_{s} + \Delta q_{mu} = 0 \
\therefore \mu p = \frac{sq^{2} p}{1 - sq} \
\text{assuming: }1 - sq^{2} \rarr 1 \
q^{2}{eq} \approx \frac{\mu}{s} \
\therefore q{eq} = \sqrt{\frac{\mu}{s}}
$$
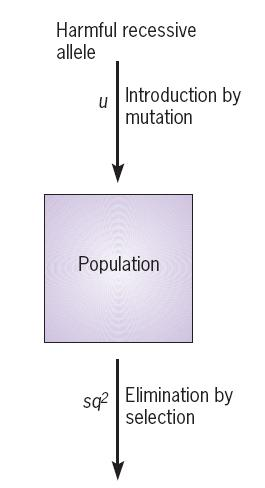
A typical value for $\mu$ is 3 x 10^6^ mutations per generation.

For s = 1, q = 0.0017
For s = 0.1, q = 0.0055,
Studies with natural populations of Drosophila have indicated that lethal alleles are less frequent than the preceding calculations predict.
Which has been attributed to partial dominance of the lethal alleles.
3. Mutation-Drift Balance
Random genetic drift eliminates variability from a population
Mutation replenishes(补充) the variability that is lost by drift