04. R <- 概率分布
一、常用概率分布函数
与分布有关的常用函数
1. seq
seq常用的参数:
| 参数 | 描述 |
|---|---|
| from | 生成向量的起点 |
| to | 生成向量的终点 |
| by | 向量元素之间的步长。默认步长为1(可修改) |
| length.out | 向量中元素数目 |
常用格式:
seq(from, to)seq(from, to, by = )seq(from, to, length.out = )seq(length.out = )
1 | |
二项分布 (Binomial)
1. 相关概念
二项分布模型处理在一系列实验中仅发现两个可能结果的事件的成功概率。例如,掷硬币总是给出头或尾。 在二项分布期间估计在10次重复抛掷硬币中精确找到3个头的概率。
- PMF: $p_{X}(k) = {n \choose k}p^{k}(1-p)^{n-k}, k=0,1,2,3,…,n$
- Expectation: $E[X] = np$
- Variance: $var(x) = np(1-p)$
Basic assumptions when we use the binomial distribution:
There are a fixed number (n) of Bernoulli trials; 有限的trial次数
The outcome of the trials are independent; 每次trial的结果相互独立
The probability of
pis constant for each trial. 每次trial的概率p不发生改变
2. 相关函数
R语言有四个内置函数来生成二项分布。 它们描述如下。
1 | |
| 参数 | 描述 |
|---|---|
| x | 数字的向量。这里表示的每一次观察对应的“x坐标”。x的长度 ≥ 1,当长度=1时,表示成功x次时候的概率;当概率为长度大于1的向量,则表示某个范围的概率值 |
| p | 概率向量 |
| n | 观察的数量,即样本量 |
| size | 试验的数量 |
| prob | 每个试验成功的概率 |
dbinom
dbinom(x, size, prob)
为了方便展示,使用plot()来进行可视化,下同。
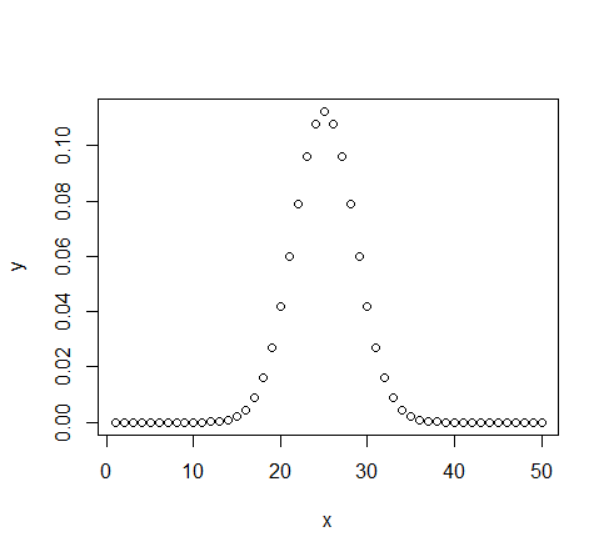
该函数给出每个点的概率密度分布。
- 返回成功
x次的概率- 若
x长度大于1,则表示某个范围的概率值
- 若
1 | |
pbinom
pbinom(x, size, prob)
此函数给出事件的累积概率。 它是表示概率的单个值。此处的概率指的是 $P(X \leq x)$。
- 若x长度为1,返回至多成功
x次的概率,即累积概率 - 若x长度大于1,则返回一个范围的值,此时为累积 (cumulative) 概率模式
1 | |
qbinom
qbinom(p, size, prob)
该函数采用概率值 ($P(X \leq x)$),并给出累积值与概率值匹配的数字。
- 返回相应分位点
x
1 | |
rbinom
rbinom(n, size, prob)
该函数从给定样本产生给定概率的所需数量的随机值。
- 返回每组试验的成功次数
1 | |
泊松分布 (Poisson distribution)
1. 相关概念
- PMF: $p_{X}(k) = \frac{\lambda^{k}}{k!}e^{-\lambda}, k=0,1,2,3,…, e \approx 2.71828$
- Expectation: $E[X] = \lambda$
- Variance: $var(x) = E[X] = \lambda$
Basic assumptions when we use the Poisson distribution:
The probability that a single event occurs within an interval is proportional to the length of the interval;
Within a single interval, an infinite number of occurrences of the event are theoretically possible, i.e. not restricted to a fixed number of trials;
The events occur independently both within the same interval and between consecutive intervals
2. 相关函数
R中有四个函数可用于泊松分布,分别是:
dpois(x, lambda):返回发生x次随机事件的概率
ppois(q, lambda):返回累积概率
qpois(p, lambda):返回相应分位点x
rpois(n, lambda):返回每组发生随机事件的次数
| 参数 | 描述 |
|---|---|
| x | 在泊松分布中即k数字的向量。这里表示的每一次观察对应的“x坐标”。 x的长度 ≥ 1,当长度=1时,表示成功x次时候的概率;当概率为长度大于1的向量,则表示某个范围的概率值 |
| q | 指定trial至多发生的次数 |
| p | 概率向量 |
| n | 观察的数量,即样本量 |
| lambda ($\lambda$) | 随机事件发生的平均次数 |
这些函数的使用方式同二项分布类似,下文不再赘述了。
例:
1 | |
正态分布 (Normal (Gaussian) Distribution)
1. 相关概念
在随机收集来自独立来源的数据中,通常观察到数据的分布是正常的。 这意味着,在绘制水平轴上的变量的值和垂直轴中的值的计数时,我们得到一个钟形曲线。 曲线的中心代表数据集的平均值。 在图中,百分之五十的值位于平均值的左侧,另外五十分之一位于图的右侧。 统称为正态分布。
Normal (Gaussian) distribution
(1) Probability
$$
P(X = k) \approx \frac{1}{\sqrt{2 \pi} \sqrt{npq}}e^{-\frac{(k-np)^2}{2npq}}
$$
(2) PDF
$$
f_{X}(x) = \frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{(x - \mu)^2}{2 \sigma^2}}
$$
(3) Mean
$$
E[X] = np
$$
(4) Variance
$$
var(X) = npq = np(1-p)
$$
(5) Standard Normal N(0, 1)
- PDF: $f_{X}(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$
- Mean: $E[X] = 0$
- Variance: $var(x) = 1$
Given that the random variable X ∼ $N(\mu, \sigma^2)$, consider the following random variable:
$$
Z = \frac{X - \mu}{\sigma}
$$
Z still follow a normal distribution
Therefore, if X ∼ $N(\mu, \sigma^2)$, then $\frac{X - \mu}{\sigma}$~N(0,1)
2. 相关函数
dnorm(x, mean, sd)
- 该函数给出给定平均值和标准偏差在每个点的概率分布的高度。
pnorm(x, mean, sd)
- 该函数给出正态分布随机数小于给定数值的概率。它也被称为“累积分布函数”。
qnorm(p, mean, sd)
rnorm(n, mean, sd)
| 参数 | 描述 |
|---|---|
| x | 在正态分布中即k数字的向量。这里表示的每一次观察对应的“x坐标”。 x的长度 ≥ 1,当长度=1时,表示成功x次时候的概率;当概率为长度大于1的向量,则表示某个范围的概率值 |
| p | 概率向量 |
| n | 观察的数量,即样本量 |
| mean | 是样本数据的平均值,默认值为零 |
| sd | 是标准偏差,默认值为1 |
使用方法同二项分布,不再赘述
二、其它概率分布函数
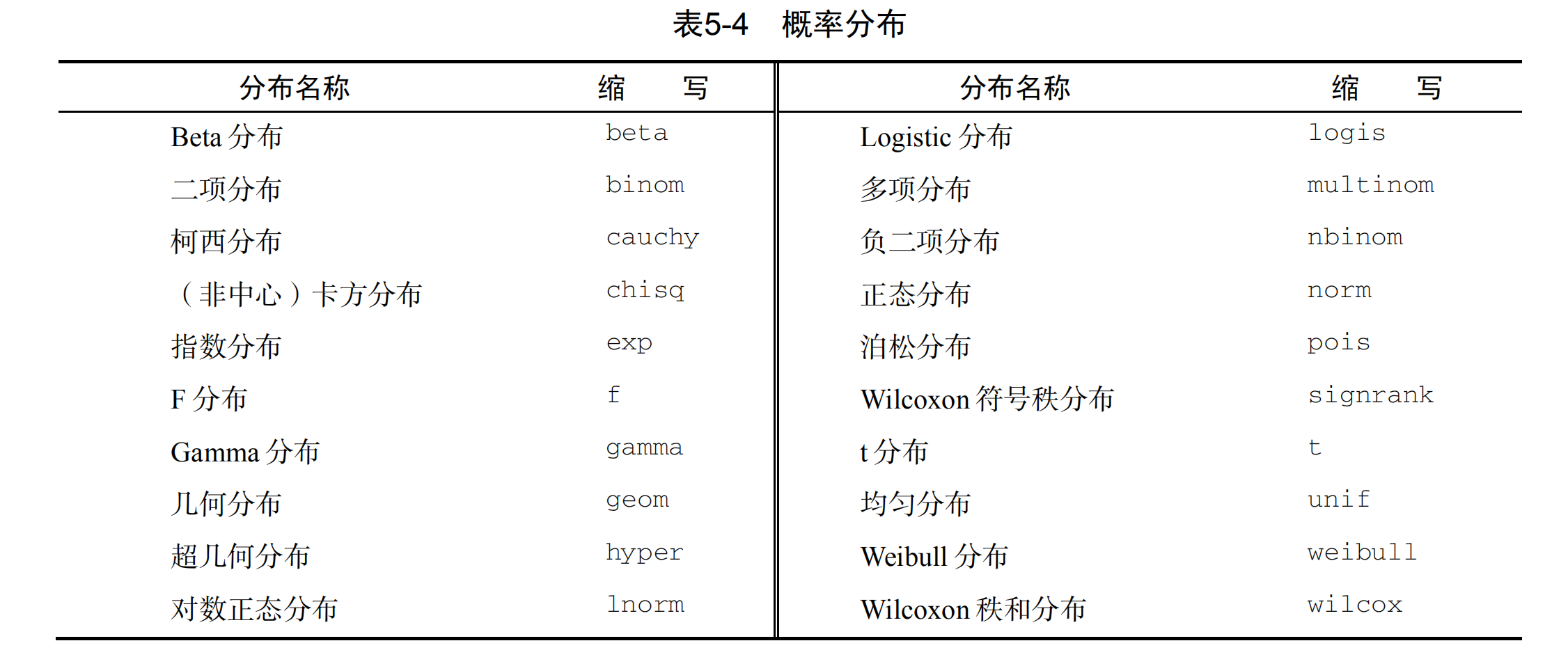
使用方法都相近:
其中第一个字母表示其所指分布的某一方面:
d = 密度函数(density)
p = 分布函数(distribution function)
q = 分位数函数(quantile function)
r = 生成随机数(随机偏差)